SPH::SmoothingKernel Namespace Reference

Functions
__device__ void	spiky (real *W, real dWdx[DIM], real *dWdr, real dx[DIM], real sml)
	Spiky kernel (Desbrun & Cani). More...
__device__ void	cubicSpline (real *W, real dWdx[DIM], real *dWdr, real dx[DIM], real sml)
	Cubic spline kernel (Monaghan & Lattanzio 1985). More...
__device__ void	wendlandc2 (real *W, real dWdx[DIM], real *dWdr, real dx[DIM], real sml)
__device__ void	wendlandc4 (real *W, real dWdx[DIM], real *dWdr, real dx[DIM], real sml)
__device__ void	wendlandc6 (real *W, real dWdx[DIM], real *dWdr, real dx[DIM], real sml)

Function Documentation

cubicSpline()

__device__ void SPH::SmoothingKernel::cubicSpline	(	real *	W,
		real	dWdx[DIM],
		real *	dWdr,
		real	dx[DIM],
		real	sml
	)

Cubic spline kernel (Monaghan & Lattanzio 1985).

With the normalization constant \( \sigma \) and dimensionality \( d \) the kernel can be defined as:

\[ \begin{equation} W(q) = \frac{\sigma}{h^d} \begin{cases} (6q^3-6q2+1) & \text{ for } 0 \leq q < \frac{1}{2} \\ 2(1-q)^3 & \text{ for } \frac{1}{2} \leq q \leq 1 \\ 0 & \text{ for } q > 1 \\ \end{cases} \quad \sigma = \begin{cases} \frac{4}{3} & \text{for } d = 1 \\ \frac{40}{7 \pi} & \text{for } d = 2\\ \frac{8}{\pi} & \text{for } d = 3 \\ \end{cases} \, . \end{equation} \]

Parameters

[out]	W	smoothed value/contribution
[out]	dWdx	spatial derivative for each coordinate axis (dimensionality: DIM)
[out]	dWdr	spatial derivative
[in]	dx	spatial separation (dimensionality: DIM)
[in]	sml	smoothing length

Definition at line 50 of file kernel.cu.

Here is the call graph for this function:

spiky()

__device__ void SPH::SmoothingKernel::spiky	(	real *	W,
		real	dWdx[DIM],
		real *	dWdr,
		real	dx[DIM],
		real	sml
	)

Spiky kernel (Desbrun & Cani).

With the normalization constant \( \sigma \) and dimensionality \( d \) the kernel can be defined as:

\[ \begin{equation} W(q) = \frac{\sigma}{h^d} \begin{cases} (1-q)^3 & \text{for } 0 \leq q < 1 \\ 0 & \text{for } q \geq 1 \\ \end{cases} \quad \sigma = \begin{cases} \frac{10}{\pi} & \text{for } d=2 \\ \frac{15}{\pi} & \text{for } d=3 \\ \end{cases} \, . \end{equation} \]

Parameters

[out]	W	smoothed value/contribution
[out]	dWdx	spatial derivative for each coordinate axis (dimensionality: DIM)
[out]	dWdr	spatial derivative
[in]	dx	spatial separation (dimensionality: DIM)
[in]	sml	smoothing length

Definition at line 14 of file kernel.cu.

Here is the call graph for this function:

wendlandc2()

__device__ void SPH::SmoothingKernel::wendlandc2	(	real *	W,
		real	dWdx[DIM],
		real *	dWdr,
		real	dx[DIM],
		real	sml
	)

Wendland C2 (Dehnen & Aly, 2012)

With the normalization constant \( \sigma \) and dimensionality \( d \) the kernel can be defined as:

\[ \begin{equation} W (q) = \frac{\sigma}{h^d} \begin{cases} (1-q)^4 (1+4q) & \text{for }d=2\text{, } d=3 \text{ and } 0 \leq q < 1 \\ (1-q)^3 (1+3q) & \text{for }d=1 \text{ and } 0 \leq q < 1 \\ 0 & q \geq 1 \end{cases} \quad \sigma = \begin{cases} \frac{5}{4} & \text{for } d=1 \\ \frac{7}{\pi} & \text{for } d=2 \\ \frac{21}{2 \pi} & \text{for }d=3 \\ \end{cases} \, . \end{equation} \]

Parameters

[out]	W	smoothed value/contribution
[out]	dWdx	spatial derivative for each coordinate axis (dimensionality: DIM)
[out]	dWdr	spatial derivative
[in]	dx	spatial separation (dimensionality: DIM)
[in]	sml	smoothing length

Definition at line 86 of file kernel.cu.

Here is the call graph for this function:

wendlandc4()

__device__ void SPH::SmoothingKernel::wendlandc4	(	real *	W,
		real	dWdx[DIM],
		real *	dWdr,
		real	dx[DIM],
		real	sml
	)

Wendland C4 (Dehnen & Aly, 2012)

With the normalization constant \( \sigma \) and dimensionality \( d \) the kernel can be defined as:

\[ \begin{equation} W (q) = \frac{\sigma}{h^d} \begin{cases} (1-q)^6 (1 + 6q + \frac{35}{3}q^2) & \text{for } d=2\text{, } d=3 \text{ and } 0 \leq q < 1 \\ (1-q)^5 (1+5q+8q^2) & \text{for } d=1 \text{ and } 0 \leq q < 1 \\ 0 & q \geq 1 \end{cases} \quad \sigma = \begin{cases} \frac{3}{2} & \text{for } d=1 \\ \frac{9}{\pi} & \text{for } d=2 \\ \frac{495}{32 \pi} & \text{for } d=3 \\ \end{cases} \end{equation} \]

Parameters

[out]	W	smoothed value/contribution
[out]	dWdx	spatial derivative for each coordinate axis (dimensionality: DIM)
[out]	dWdr	spatial derivative
[in]	dx	spatial separation (dimensionality: DIM)
[in]	sml	smoothing length

Definition at line 118 of file kernel.cu.

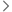Here is the call graph for this function:

wendlandc6()

__device__ void SPH::SmoothingKernel::wendlandc6	(	real *	W,
		real	dWdx[DIM],
		real *	dWdr,
		real	dx[DIM],
		real	sml
	)

Wendland C6 (Dehnen & Aly, 2012)

With the normalization constant \( \sigma \) and dimensionality \( d \) the kernel can be defined as:

\[ \begin{equation} W (q) = \frac{\sigma}{h^d} \begin{cases} (1-q)^8 (1 + 8q + 25 q^2 + 32 q^3) & \text{for } d=2\text{, } d=3 \text{ and } 0 \leq q < 1 \\ (1-q)^7 (1 + 7q + 19 q^2 + 21 q^3) & \text{for } d=1 \text{ and } 0 \leq q < 1 \\ 0 & q \geq 1 \end{cases} \quad \sigma = \begin{cases} \frac{55}{32} & \text{for } d=1 \\ \frac{78}{7 \pi} & \text{for } d=2 \\ \frac{1365}{64 \pi} & \text{for } d=3 \\ \end{cases} \, . \end{equation} \]

Parameters

[out]	W	smoothed value/contribution
[out]	dWdx	spatial derivative for each coordinate axis (dimensionality: DIM)
[out]	dWdr	spatial derivative
[in]	dx	spatial separation (dimensionality: DIM)
[in]	sml	smoothing length

Definition at line 152 of file kernel.cu.

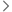Here is the call graph for this function: